(Adapted from 100 LAST Orchestration Tips, planned for release in late 2026)
Despite the emphasis by orchestration manuals on the clarinet’s odd-numbered overtones, both in character of tone and in overblowing, even-numbered overtones also play a key role in the shaping of the clarinet’s unique timbre.
There is no question that odd-numbered partials dominate the essence of a clarinet’s tone and functional operation. This is rightly stressed by orchestration manuals attempting to impart a basic understanding to their readers from the first page – pointing to the clarinet’s cylindrical body as the source of this phenomenon. Some more in-depth tomes will discuss how this construction simulates a closed-pipe construction, which in turn allows a shorter length of pipe to produce lower typical fundamentals, inch-for-inch, as compared to an open-pipe instrument such as the oboe.
But the core takeaways are that the clarinet sounds the way that it does because its tone is “rich in odd-numbered partials” (meaning that the 1st, 3rd, 5th, 7th, 9th etc. overtones tend to predominate) – and that the instrument is, in fact, only capable of satisfactorily overblowing across these odd-numbered partials. This usually leads to a discussion of how this held the clarinet back from becoming a standard member of the orchestra until certain mechanical problems were solved in the Late Classical period, the biggest of which being how the player was to finger an octave-and-a-half of fundamental tones (i.e. 11-12 diatonic pitches) with only 8 fingers and a thumb. If there ever was a woodwind family whose identity as a perfected modern instrument relied the most strongly on a system of keywork, it would be the clarinets.
The chart below spells out this whole peculiar system of odd-partial overblowing – though be aware that for altissimo register pitches, there are a number of different fingerings and overblowing strategies, sometimes dependant on different keywork systems. The example here just represents some of the most typical. The clarinet has an enormously generous array of 1st-partial fundamental tones, from a low written E3 to a B-flat 4. These are divided into two groups, the first of which is a basic F major scale across which the fingers naturally sit, plus the 1/2 step below of that low E extension. This is usually referred to as the “chalumeau” register. The top 4 pitches represent the “throat tones,” a series of pitches that close the gap between the top F or F-sharp of the chalumeau and the first pitch of the next register, called the “clarino” (aka “clarion” in English-language parlance). Notice the overblowing to the 3rd partial of an octave+5th: each pitch from B4 up to C6 sits on a fundamental tone of the chalumeau register. The relationship between the two registers gives the clarinet its very wide range of colour; the generously rich, reedy basement of fundamental tones contrasting with the more incisive, penetrating upper-register timbre, whose name “clarino” essentially means “trumpet.” Then upward from here, the odd-numbered partial overblowing continues through another octave of tones, becoming ever more thin and piercing in character. The chart here shows 5 semitones from C-sharp6 up to F6 of 5th-partial overblowing, playing two octaves + a Major 3rd above the chalumeau tones of A3 to C-sharp4. Then 7th-partial overblowing, 2 octaves + a minor 7th above the fundamental tones gives the player another 5 semitones from F-sharp6 to B-flat 6 (here’s where fingering and keywork can differ the most between different players and models of instrument). The top two pitches of written B6 and C7 are accessed, at least according to this chart, as 9th-partial tones overblowing a soaring 3 octaves + a Major 2nd above the chalumeau root tones.

Naturally, this baked-in overblowing of odd-numbered partials also means that their character will dominate most of the instrument’s range of pitches. So much so that I’ve observed a kind of misperception creep into discussions of the clarinet’s overtones, in which only the odd-numbered partials play any role whatsoever. One conversation over which I eavesdropped included the claim that there weren’t any even-numbered partials at all (!) – and I must admit in some exchanges I myself have somewhat soft-pedalled the presence of anything besides odd-numbered partials.
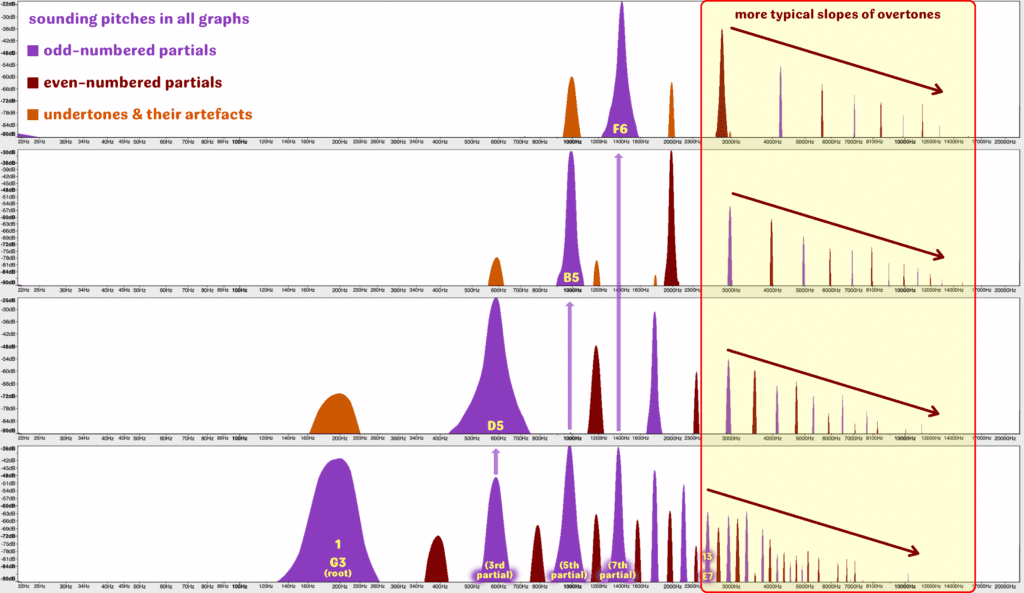
And yet all one has to do is look at a spectrograph of a clarinet waveform in order to observe the presence of a fully-inhabited tone with all the expected overtones, both odd and even. Let’s select one of the most generous and stable of the chalumeau pitches: Written A3, over which an overblown pitch is present in every slot all the way up to the 9th partial. On a B-flat clarinet, this is sounding G3 – so let’s start with a spectrograph of that pitch. Below, we see how the misperception of the even-numbered partials’ absence arises: the peaks of the first 6-7 odd-numbered partials stand around twice as high as their even-numbered neighbours. This is the source of descriptions of clarinet tone as being “hollow,” “lean,” or even “hooting.” What’s suppressed is even more telling than what’s emphasised. A chalumeau register tone will lack strength at the first and second octave above the root, the outside partials of what I call the “body of tone; not to mention a third weak octave above that. The powerful 3rd-partial D5 and 5th-partial B5 are echoed weakly above in the even-partial D6, B6, and D7. This puts the emphasis of timbre on a widely-spaced 13-sharp11 chord – a tone that for all its lack of lower thickness still has a wonderfully open, radiant character.
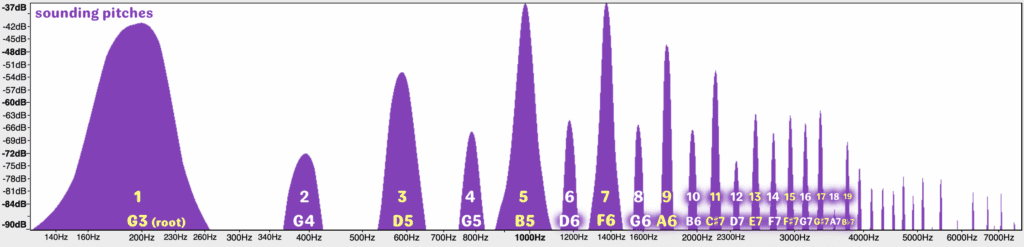
One thing you may notice in the chart above: from the 13th partial upwards, the strength of all the partials is more of a parlimentarian democracy and less of a dictatorship. Most partials within certain regions are more or less equal in strength – with some underrepresented minorities like the 18th partial to be sure – but in higher areas of this upper sheen of tone, we also see some odd-numbered partials gapping out here and there. Put a pin in this, because this timbral equality will become more relevant as we progress.
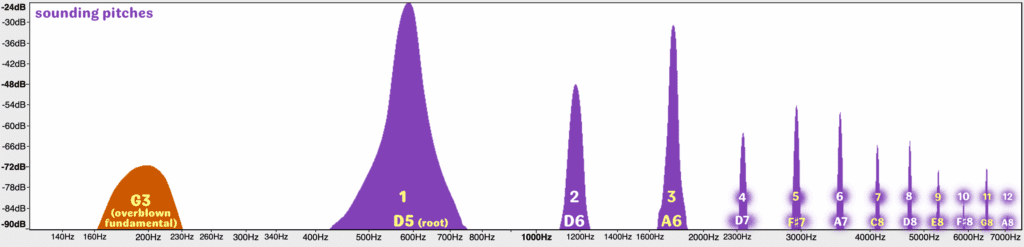
So now let’s look at the first overblown pitch above that root tone of sounding G3/written A3: sounding D5/written E5. We see a strong resemblance to the previous spectrograph: with massively powerful 1st, 3rd, and 5th partials surrounding comparatively weaker 2nd and 4th partials covering the first and second octave above the root tone. We can also see a sizeable lump under everything, the original G3 chalumeau fundamental serving as a subtle undertone. But notice something much more significant at the other end of the graph: past the 5th partial, the even-numbered partials are much more present, playing a more-or-less equal role in the downward slope of the remaining sheen of tone. Granted, we see some gaps at the 10th and 12th partials, but the general trend is more of an equality of timbral function. And what’s the outcome of all this? Simply that while the basic thrust of the timbre will be similar to the chalumeau’s gaunter tone, the radiance of the sheen will be brighter and more trumpet-like or oboe-like in flavour. So here at the first level of overblowing, we see already that the even-numbered partials have much to add to the clarinet’s essential character. Hence the clarino register’s titular relationship to the trumpet is built right into its upper partials.
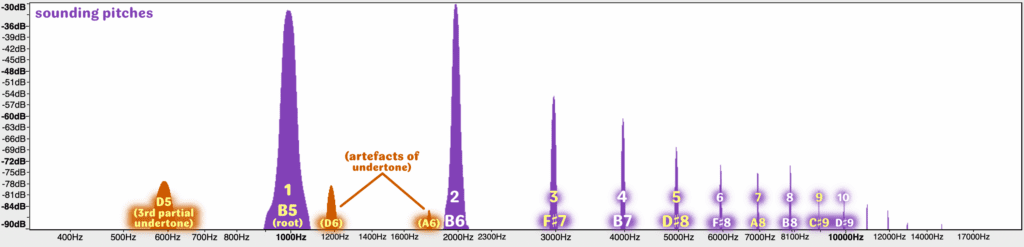
It’s been generally observed that at higher and higher extreme pitches amongst the standard winds, the individuality of each instrument’s character becomes less and less pronounced, and more similarly thin and piercing. In the clarinet’s case, at least, it’s easy to see why: overblowing to a sounding 5th-partial B5/written C-sharp, the dominance of odd-numbered overtones relinquishes, with the second partial as strong or stronger than the root, and the rest of the overtones sloping more regularly away just like any other high wind instrument such as oboe or flute. Some clarinet family character seeps in from below, almost imperceptibly from the 3rd partial undertone – which in turn creates its own overtones which we see as artefacts in the graph. This effect will be subtle, almost negligible – but will still add enough quality of tone to help the ear differentiate the tone from other winds to a degree.
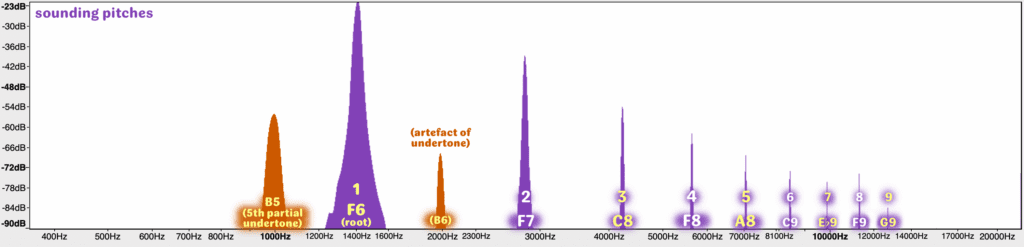
This pattern simply continues as we continue higher with our overblowing from that original chalumeau fundamental. Ascending to the 7th partial now, the resulting sounding pitch of F6/written G6 has an even more regular slope from root tone upwards. The odd- and even-numbered partials have no particular role to play relative to one another in distinguishing the timbre – and yet we see the 5th-partial undertone and its own overtone contributing to the equation with at least the same strength as the 4th and 5th partials. So while they won’t be heard as pitches in and of themselves, their colour will still keep the clarinet’s identity to some degree individual.
This taming of odd-numbered partials in the altissimo register is really a secondary phenomenon. The vast majority of pitches written for clarinet will be over those registers in which odd-numbered partials are at their most prominent – the chalumeau and clarino. So the general observations quoted at the beginning of this tip still ring true. And yet one might well ask – why does the clarino register’s sheen of tone so quickly conform to a more typical balance of partials? And why does the altissimo register stray even further away from odd-numbered partial dominance? For the answer, it’s useful to stack all of these spectrographs on top of one another, tinting the even-numbered partials red for reference, and looking at how each higher overblown note is in a sense a curtailed version of the fundamental tone at the bottom. If, as we saw in Ex. 2, the partials trend more equal in strength from the 13th partial in the chalumeau register, then the slope of each higher pitch’s overtones will follow the same trend above regardless of the overblown root tone.
Don’t let the technicalities fool you into thinking that this is all academic. Instead, consider the implications, and how what we might consider as instinctive in some circumstances has a very easy-to-grasp practical basis at its heart. For instance – the observation that unison trumpets and clarinets can be powerfully penetrating and dramatic in high, emphatic scoring; and yet the difficult intonation and blending of tone that vexes clarinetists comes right out of what we see in Ex. 3. The beautifully matching sheen of tone may shout splendidly in unison, yet the odd-numbered partials have a different kind of precise centre of intonation compared to the trumpets. Another implication is how this general trend in overtones affects the use of auxiliaries. The bass clarinet’s silvery tone when played softly across its upper range is a beautiful match with low-to-middle-register flutes precisely because its overtones are more balanced rather than overly dominated by odd-numbered partials. And then on the other hand, the shallowness of C, D, and E-flat clarinets is precisely due to the strength of odd-numbered partials having elevated dominance at higher and higher pitches, all while the increasingly narrow bores of these instruments further lighten the depth of tone.









